Simultaneous Localization and Mapping (SLAM) Mining Agent

    Below are recordings of a mining agent that I'd programmed to use an online graph slam algorithm to maintain its position in space while discovering its surroundings using sensor data. This is the final project of the "Artificial Intelligence for Robotics" graduate course at Georgia Tech.

    The red point is the agent's position. The grey points are gems to be mined, with the gem types (letters) above them. The black point is the agent's next destination. The agent needs to explore the space (which it does using an achimedian spiral) until finds and extracts all the gems of specific types that it requires. When it finds any gem, it can use as a reference point for its position for future movement.

    The agent gets data from noisy movement and landmark distance sensors and updates a graph of Omega (weights) and Sigma (scalars) matrices with the information. With each movement step, the online algorithm extends the matrices to integrate the information and then removes the old movement data, reducing the matrix sizes back to its prior size. This ensures that the graph will never grow too large regardless of the number of timesteps.

Examples of Omega and Sigma used to calculate Mu position estimates vector

    Similar to a Kalman filter, the graph slam algorithm works via the gaussian equation, however graph slam extends the equation to use a matrix to handle multiple constraints. This allows the agent to explore the space, adding new information about landmarks and movement (mapping) to the matrix while using prior and current instrument measurements to maintain where the agent is in this mapped space (localization).

Gaussian equation 

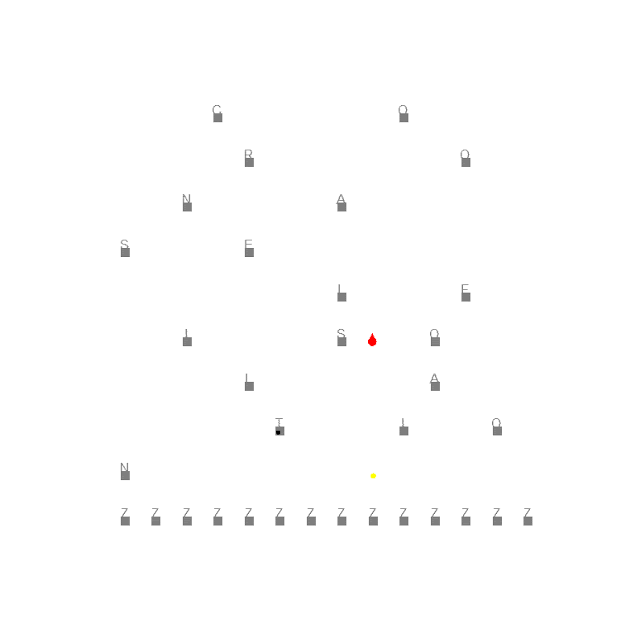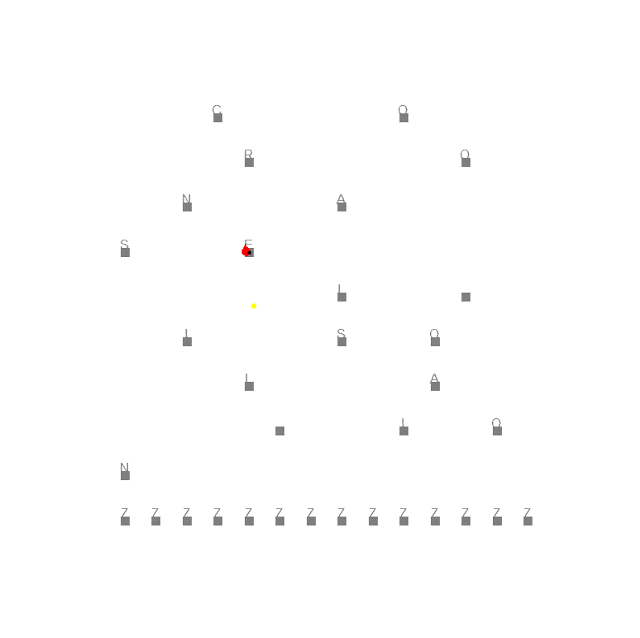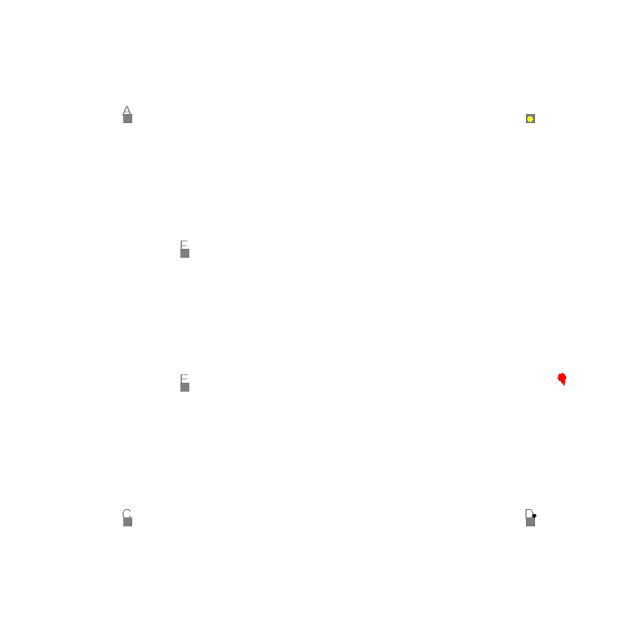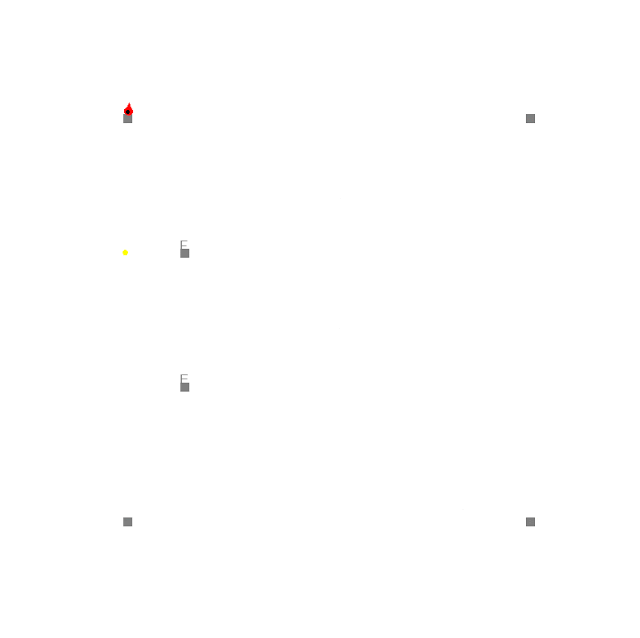
Particle Filter to Determine 3D Position from Noisy Height Sensors

    Below are recordings of a "Mars Rover" agent that I'd programmed to determine its position and successfully navigate itself to the goal point using a particle filter. This is part of the "Artificial Intelligence for Robotics" graduate course at Georgia Tech.

    The agent builds a collection of particles with randomized parameters based on sensor noise and environment variables. It then weights the viability of each particle using a probability density function with the absolute height and radar to ground height. It resamples from the particle pool with replacement based on the weights, propagates them forward in time according to the agent's movement model, and randomizes some of the variables further.

    Once the particles have converged to a point that the standard deviation between their locations is low enough, the agent uses a weighted average of the particles to estimate its position. With this position, the agent calculates the turning angle to get to the goal point.

    The code for the mars rover and rendering was provided by GaTech; the code for the particle filter and ship's navigation strategy was written by me.

Add caption

Detection of the agent's position and navigation to goal point. 

Agent is red, particles are green/black, estimation is purple.

Detection of the agent's position, showing terrain height visualization. 

Agent is red, particles are green/black, estimation is purple.

Hyperparameter tuning based on trail runs (blurred for Academic Honesty Policy)

Kalman Filter to Navigate Obstacles Based on Noisy Senor Data

I've implemented a Kalman filter that takes noisy sensor data regarding the x and y positions of the asteroids in this simulation to infer the velocity and acceleration based on the bivariate normal distribution. This data is used to navigate a ship from the bottom to the top of the screen, avoiding all of the asteroids by using their predicted future positions. This is part of the Artificial Intelligence for Robotics course for the CS Master's program at Georgia Tech.

The Kalman filter is ideal for this application because of its ability to handle noisy data by using the Kalman gain to gradually transition from relying on the sensor to the internal model and because of its ability to infer correlated variables such as velocity and acceleration using a transition function that can define the physical constraints of the system. Because this system uses 6 variables it requires the use of linear algebra matrix operations vs the more 1D application of the Kalman filter.

The ship uses the predicted future positions of the asteroids to, at any given timestep, determine if steering left, right, or center, would bring to nearer or father from the squared euclidean distance of the future position of the nearest asteroid.

Below are samples of the ship using the Kalman filter to avoid the asteroids and reach the goal. The code for the asteroid field and rendering was provided by GaTech; the code for the Kalman filter and ship's navigation strategy was written by me.